1. Подсчитать, сколько места будет занимать одна минута цифрового звука на жестком диске или любом другом цифровом носителе, записанного с частотой а) 44.1 кГц; б) 11 кГц; в) 22 кГц; г) 32 кГц и разрядностью 16 бит.

Решение.

а) Если записывают моносигнал с частотой 44.1 кГц, разрядностью 16 бит (2 байта), то каждую минуту аналого-цифровой преобразователь будет выдавать 441000 * 2 * 60 = 529 000 байт (около 5 Мб) данных об амплитуде аналогового сигнала, который в компьютере записываются на жесткий диск. Если записывают стереосигнал, то 1 058 000 байт (около 10 Мб).

б) для частот 11, 22, 32 кГц расчеты производятся аналогично.

---

2. Какой объем данных имеет моноаудиофайл, длительность звучания которого 1 секунда, при среднем качестве звука (16 бит, 24 кГц)?

Решение. 16 бит * 24000 = 384 000 бит = 48 000 байт = 46 875 килобайт.

---

3. Рассчитайте объем стереоаудиофайла длительностью 20 секунд при 20-битном кодировании и частоте дискредитации 44.1 кГц.

Решение. 20 бит * 44100 Гц = 882000 бит/с = 110250 байт/с = 107,67 Кб/с,

              107, 67Кб/с *20 с = 2153,32 Кб,

              т.к. дан стереоаудиофайл, то полученное значение надо умножить на 2

               2153,32Кб * 2=4306,64Кб = 4,21 Мб 

---

4. Определите количество уровней звукового сигнала при использовании 8-битных звуковых карт.

Решение: 28 = 256 уровней

---

5. На рисунке изображено зафиксированное самописцем звучание 1 секунды речи. Закодируйте его в двоичном цифровом коде с частотой 10 Гц и длиной кода 3 бита.  

Решение:

Кодирование с частотой 10 Гц означает, что мы должны измерить высоту звука 10 раз за секунду. Выберем равноотстоящие моменты времени:

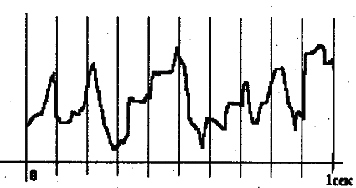
Длина кода в 3 бита означает 23 = 8 уровней квантования. То есть в качестве числового кода высоты звука в каждый выбранный момент времени мы можем задать одну из следующих комбинаций: 000, 001, 010, 011, 100, 101, 110, 111. Их всего 8, следовательно, высоту звука можно измерять на 8 «уровнях»:

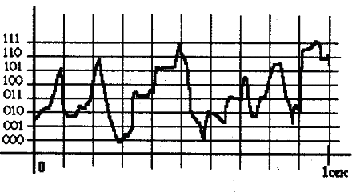
«Округлять» значения высоты звука будем до ближайшего нижнего уровня квантования (горизонтальное деление) в выбранный момент времени (вертикальное деление):

Используя данный способ кодирования, мы получим следующий результат (пробелы поставлены для удобства восприятия): 100 100 000 011 111 010 011 100 010 110.

Примечание.

Целесообразно обратить внимание на то, насколько неточно код передает изменение амплитуды. То есть частота дискретизации 10 Гц и уровень квантования 23 (3 бита) слишком малы. Обычно для звука (голоса) выбирают частоту дискретизации 8 кГц, т. е. 8000 раз в секунду, и уровень квантования 28 (код длиной 8 бит).

Ответ: 100 100 000 011 111 010 011 100 010 110.